whlit's blog

Appearance

B树与B+树 ​

B树 ​

B树是一种平衡的多叉树，即查找路径不止两个。

B树B树可视化演示

通常我们说m阶的B树，它必须满足如下条件：

  • 每个节点最多只有m个子节点。
  • 每个非叶子节点（除了根）具有至少 m/2 子节点。
  • 如果根不是叶节点，则根至少有两个子节点。
  • 具有k个子节点的非叶节点包含 k-1 个键。
  • 所有叶子都出现在同一水平，高度一致。
  • 所有节点的键值是升序排列的。

m阶：指一个节点的子节点个数的最大值。

键：指节点中的键值。最大个数为 m-1。

查询 ​

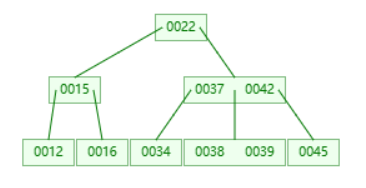
以上图的示例查询38为例：

  1. 从根节点开始，根节点的键值是22，22<38，所以进入根节点的右子节点。
  2. 节点的键值是[37,42]， 37< 38 < 42，所以进入该节点的中间节点。
  3. 节点的键值是[38,39]， 38=38，所以返回该值。

插入 ​

以上图的示例插入40为例：

  1. 从根节点开始，根节点的键值是22，40>22，所以进入根节点的右子节点。
  2. 节点的键值是[37,42]， 37< 40 < 42，所以进入该节点的中间节点。
  3. 节点的键值是[38,39]， 39 < 40，由于该节点为叶节点，所以插入后面，键值为[38,39,40]，保证键值升序排列。
  4. 由于该树为3阶，所以插入后，节点的键值个数超过2个，需要分裂。
  5. 将分裂的键插入到父节点。如果插入后父节点的键值个数超过2个，则需要分裂。重复该步骤。
  6. 插入后，根节点的键值个数超过2个，需要分裂并创建新的根节点。将分裂后的节点插入到新的根节点上。

分裂逻辑

  1. m阶的B树分裂时，需要将该满个数的节点的后 m/2 个键分裂出来创建新的节点
  2. 剩余的键值的最大值，也就是最后一个键值，需要插入到父节点中。
  3. 其他的键值作为原有的节点的键值。

具体可以查看《算法导论》第283页B树的分裂逻辑。

例如

上面的示例中[38,39,40]这个节点需要分裂，则将[40]创建新的节点，[39]提取到父节点中，[38]作为原有节点的键值。

如果是4阶的树，有节点[38,39,40,41]需要分裂，则将[40,41]创建新的节点，[39]提取到父节点中，[38]作为原有节点的键值。

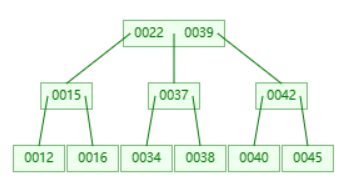
插入后的树结构如下：

插入后

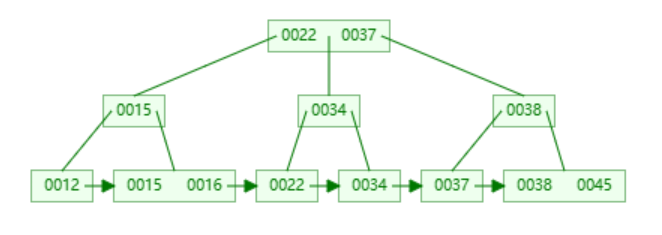
B+ 树 ​

B+树是在B树基础上进一步改近得到的。B+树的非叶子节点不存储数据，只存储指关键字的指针，所有数据都保存在叶子节点。所有的叶子节点是从小到大排列的有序链表。

B+树

插入 ​

  1. 如果为叶子节点则直接插入，如果非叶子节点，向下查找，直到找到叶子节点，然后插入。
  2. 如果插入后叶子节点的键值个数超过 m-1 ，则需要分裂。第 m/2 +1 值的键向上插入到父节点。
  3. 如果插入后父节点的键值个数超过 m-1 ，则需要分裂。第 m/2 值的键向上插入到父节点。

分裂逻辑

  • 叶子节点
  1. 分裂的节点中左节点包含前 m/2 个值，右节点包含剩下的值。
  2. 第 m/2 + 1 个值的键向上插入到父节点。
  3. 将叶子节点的左右叶子节点的链接更新。
  • 非叶子节点
  1. 分裂的节点中左节点包含前 m/2 个键，右节点包含 m/2 + 1 之后的键。
  2. 第 m/2 + 1 个键向上插入到父节点。

B+树的优势 ​

  1. B+树查询更稳定，由于B+树的数据都存储于叶子节点上，所以每次查询都是相同的路径长度。
  2. B+树具备排序性，B+树中所有的叶子节点是一个有序的链表。
  3. B+树遍历更快，由于所有的数据都存储于叶子节点上，所以遍历树只需要遍历叶子节点的链表即可。

参考 ​